摘要
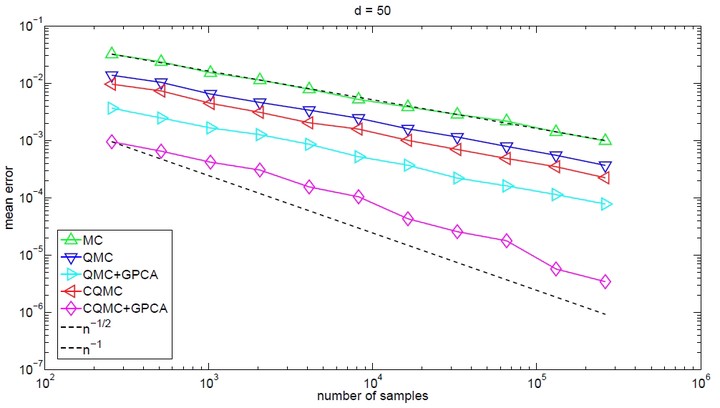
This paper studies the rate of convergence for conditional quasi–Monte Carlo (QMC), which is a counterpart of conditional Monte Carlo. We focus on discontinuous integrands defined on the whole of $\mathbb{R}^d$, which can be unbounded. Under suitable conditions, we show that conditional QMC not only has the smoothing effect (up to infinitely times differentiable) but also can bring orders of magnitude reduction in integration error compared to plain QMC. Particularly, for some typical problems in options pricing and Greeks estimation, conditional randomized QMC that uses $n$ samples yields a mean error of $O(n^{-1+\epsilon})$ for arbitrarily small $\epsilon>0$. As a byproduct, we find that this rate also applies to randomized QMC integration with all terms of the analysis of variance decomposition of the discontinuous integrand, except the one of highest order.